Analysis of a brilliant rendition Jalajaksha

The long weekend spent in Santa Barbara bore fruit, thanks to my pal, Karthick Santhanam. During our drive over Camino Cielo, we were dumbstruck, partly by the beautiful mountains and partly by Dr. L. Subramaniam‘s virtuoso on the violin. For people who don’t know about this acclaimed artist, he is one of the pioneers in the world of music and is one of the very few artists who is adept with both the Carnatic and Western styles of playing the violin. For people who need a taste of what he is capable of, please listen to this. Apologies for the lack of sync between the audio and the video!

I’ve always wanted to write about carnatic music, whenever I felt disappointed by the fact that a friend of mine doesn’t appreciate it. I never did. But, thanks to Dr. L. Subramaniam, I’m writing this (and hopefully many more posts introducing carnatic music to an untrained listener aiming to help him appreciate the beauty of this wonderful art – Psst! But don’t tell anyone because I’m aware of my laziness! :)). Carnatic music is known for its brilliant mix of kalpita (the artist sings someone’s composition) and kalpana (the artist’s own creative component). Any concert has a great deal of the kalpita and kalpana. Though it requires a lot of practise and skill to execute the kalpita component, the ultimate test to an artist is to execute the kalpana component with panache.

If you didn’t sit through the 33 minute rendition, here are some tidbits for you. The song is Vatapi Ganapathim by Sri Muthuswami Dikshithar in the raga Hamsadwani and set to the Aadi tala. More about Ragas and Talas in a different post. Believe me, the talas are one beautifully laid out system which I hope will be apparent by the end of this post. This post is a simple analysis of the tala system (and the math behind it) used by Dr. L. Subramaniam in one of his renditions of Jalajaksha, a varnam in the same raga Hamsadwani, composed by Sri Maanampuchaavadi Venkata Subbaiyyar. This was the song that made us (myself and Karthick) open-jawed for almost 13.5 minutes during our drive on Camino Cielo. The song is on Spotify and you can find it here. I couldn’t find a version on YouTube! 😦 Even if you didn’t listen to the YouTube link, please listen to this and I assure you that a Spotify account is definitely worth it. The rendition is almost 15 minutes long of which the first 13.5 minutes made us sweat before we could realise what was going on.

Righto! Here it goes. To understand mathematically what is going on, I shall explain briefly about the concept of tala. The tala is the tempo of a song. A tala is usually a repeating pattern of beats to which a song is set. There are several talas in carnatic music, of which a majority of varnams (a type of song which typically has 2 major stanzas, a swara stanza, a smaller stanza followed by 4-5 swara stanzas again) are in a tala called Chatusra-jaati Triputa tala, fondly known as the Aadi tala. A majority of Indian film songs (even a lot of western ones) are also in Aadi tala. There are 8 beats in the tala which repeat over and over. Try singing a film song with beats counting from 1 to 8 and chances are that the song’s stanzas will perfectly fit in a window of 8 beats. This window of 8 beats is known as the aavarthanam or the time frame. Each beat holds actually a defined number of swaras, i.e. between two successive beats, a defined number of swaras can be crammed. This is known as the nadai of the tala. The time between two successive beats is called the __kaala-pramaanam __(KP). In tisra nadai, there are 3 swaras per beat and hence 24 swaras for a KP. In chatusra nadai, there are 4 swaras per beat and hence 32 in a KP. In kanda nadai, there are 5 swaras per beat and hence 40 in a KP.  In misra nadai, there are 7 swaras per beat and hence 56 in a KP. In sankeerna nadai, there are 9 swaras per beat and hence 72 in a KP. Phew! So, the 5 nadais mentioned here are the basic building blocks. But, we aren’t done yet. These nadais have higher speeds. The ones mentioned are the lower most speeds and the higher speeds are in multiples of 2. So, speed i in a nadai with n swaras per beat will have n*2^(i-1) swaras per beat.

So what’s so brilliant in this, you ask! It’s just some basic math. The brilliance rests in how these are used in a song and a varnam is an excellent type of song where an artist’s tala nyaanam is put to test.

Before we move further, another digression about the song Jalajaksha. The first stanza (pallavi) of the song comprises of 2 aavarthanams (which equals the number of sub-stanzas) in the chatusra nadai. The second stanza (anupallavi) comprises of 2 aavarthanams and the third (mukthayi swaram) comprises of 4 aavarthanams. Hence, we need at least 8 __aavarthanams i__n the chatusra nadai to sing the first three stanzas. And thus 8 * 8 beats per aavarthanam * 4 swaras per KP = 256 swaras. It should be noted that the KP is always constant, no matter what nadai the song is currently sung in.

Dr. L. Subramaniam’s rendition of Jalajaksha begins just like a normal rendition, during which he plays the pallavi, anupallavi and the mukthayi swaram (the first three stanzas) in the chatusra nadai. An __aavarthanam __(8 KPs) takes about 13 seconds to complete in which 32 swaras are played. And bear in mind that, whatever nadai a song is played in, the KP always remains the same. It is the reference against which the entire song is played. The three stanzas take up 8 aavarthanams and by about 105 secs (~13*8), the __chatusra __nadai completes. A usual rendition will do the chatusra nadai in the second speed which would comprise of just 4 aavarthanams (simple math here, everything is sped to 2x – each beat now comprises of 8 swaras and the three stanzas take up half of the aavarthanams used for the first speed).

But, Dr. L. Subramaniam is no usual person. Indeed he takes up the 2x version of chatusra nadai, but not until he’s done with exploring the other nadais and making the listener sit in awe. So, after 4 swaras per beat, the next in line is 5 swaras, which is the kanda nadai. You might be wondering why the tisra nadai was omitted. Well, actually not. The song being originally in chatusra nadai, the next multiple of 3 being 6 will be the tisra nadai 1x.

With kanda nadai, we are in a position to cram in 256 swaras in a multiple of 5 positions. Which isn’t possible if we want to end the nadai in an aavarthanam. The trick is to repeat one or more of the sub-stanzas so that we end up in a multiple of 5 swaras. Dr. L. Subramaniam repeats the entire pallavi one more time which would mean that there are 4 + 2 + 4 = 10 sub-stanzas. But, as we cram 5 swaras in a beat, instead of the usual 4, a sub-stanza would complete in 4/5th of an aavarthanam. Thus we would have 10*4/5 = 8 aavarthanams. And thus 8 * 8 beats * 5 swaras per KP = 320 swaras.

The next in line is a beat with 6 swaras, the tisra nadai. Here, we are in a position to cram in 256 swaras in a multiple of 6. The trick would be to repeat only one of the sub-stanzas, say the first sub-stanza of the pallavi. Thus, we would have 3 + 2 + 4 = 9 sub-stanzas. And, a sub-stanza would complete in 4/6th of an aavarthanam. Thus we would have 9*4/6 = 6 aavarthanam. And thus 6 * 8 beats * 6 swaras per KP = 288 swaras. Voila!

The next logical step is to cram in 7 swaras in a beat, the misra nadai. We need to cram 256 swaras in a multiple of 7. Repeat everything except the last two sub-stanzas of the third stanza. Thus we would have 4 + 4 + 6 = 14 sub-stanzas. And a sub-stanza would complete in 4/7th of an aavarthanam. Hence, 14*4/7 = 8 aavarthanams. Thus 8 * 8 * 7 = 448 swaras.

The 5th version is to cram 8 swaras in a beat, the chatusra nadai in 2x! This should be fairly simple with 4 aavarthanams and everything being sung just once, because 256 is a multiple of 8 as well! Hence, there are 256 swaras.

The 6th is to cram 9 swaras, the sankeerna nadai. And, 288 is a multiple of 9! So,  we would have 3 + 2 + 4 = 9 sub-stanzas completing in 4/9th of an aavarthanam, having a mere 4 aavarthanams. And 288 swaras.

The 7th is to cram 10 swaras, the kanda nadai in 2x, which would complete in 4 aavarthanams, having 320 swaras.

Interestingly, the 8th would not be 11 swaras. The above given nadais are the building blocks and hence there is no purported ekaadasha nadai. However, some accomplished artists on rare occasions, try an ekaadasha nadai in a type of rendition called the Ragam Tanam Pallavi, a pinnacle kalpana component! So, the 8th would be 12, which is tisra nadai in 2x. This would complete in 3 aavarthanams, having 288 swaras.

The next will not be 13, for the same reason as 11 swaras. Here’s a spoiler – no more prime numbers! 😦 So, we’ll have 14 swaras, which is misra nadai in 2x. This would complete in 4 aavarthanams with 448 swaras.

Following this, we’ll not have 15 as kanda nadai in 3x, because remember that speeds are related to each other by powers of two! The next speed would be 4x and there is no 3x! So, we’ll have 16 as chatusra nadai in 4x, which would mean that we’ll have 2 aavarthanams with 256 swaras.

The next nadai will be 18 swaras in a beat which will be sankeerna nadai in 2x. This has 2 aavarthanams with 288 swaras.

The next will be 20 swaras which is kanda nadai in 4x, in 2 aavarthanams with 320 swaras.

And finally, there is the tisra nadai in 4x with 24 swaras, in 2 aavarthanams with 384 swaras.

After this, Dr. L. Subramaniam finishes and starts the 4th stanza, the charanam and does the final swara stanzas (chittai swarams) in the chatusra nadai in 2x.

Now, you might wonder why he didn’t go further. He certainly is a superman and could’ve gone further. But during the last nadai, he played 2 aavarthanams amouting to about 27 (~13*2) secs and he crammed 384 swaras in them. So, the time for each swara would have been 27/384 = ~ 70 ms! That’s God Speed, on a violin! Just a mere 70 ms for a single swara! And they thought that neutrinos (might!) travel faster than light! 😛

Now for some fantasy. Had he gone further, the next nadai would have been 28 swaras which would be misra nadai in 4x, time for each swara would be 27/448 = ~ 60 ms. Next would be chatusra nadai in 8x, time for each swara would be 13/256 = ~ 51 ms. Following that would be sankeerna nadai in 4x, time for each swara would be 13/288 = ~ 45 ms. And then would be kanda nadai in 8x, time for each swara would be 13/320 = ~ 41 ms. Next would be tisra nadai in 8x, time for each swara would be 13/384 = ~ 34 ms. And that would be it (ideally) because the next one would be misra__ nadai__ in 8x, but that would take only 1/2 aavarthanam. One could technically sing everything one more time to arrive at an integral number of aavarthanams, but nobody is known to have done that, at such a high speed!

This is a perfect exhibition of an exponential series. This is evident from the lengths of each sub-stanza in each of the iterations. The measurements of lengths aren’t accurate, hence the jaggedness.

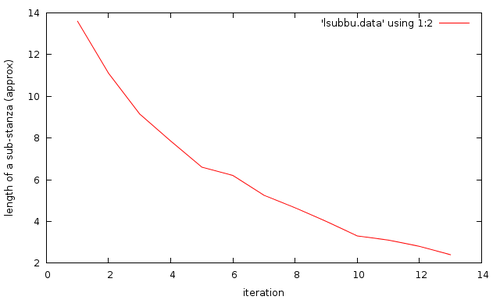
So, the series is {1, 2, 3}, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, 24, 28, 32, 36, 40, 48, 56, 64, 72, 80 … swaras per beat. This is the sequence A103969 according to oeis.org. These numbers are the common numbers between the Doudna sequence and the inverse of the Doudna sequence.

So, here are some questions for which I’m yet to arrive at concrete answers. Do comment if you have answers to these.

1. Why exactly are nadais of 11, 13 etc. not used?
2. How cool would it be to sing the nadais of only primes? Has any singer in the past attempted it?
3. I believe only ___n___x is allowed, where n is a power of two because no two speeds of nadais will coincide. Correct me if I’m wrong.
4. What are Doudna sequences?